皮亚诺曲线(英语:Peano Curve,也称:希尔伯特曲线,Hilbert Curve)是一条能够填满正方形的曲线。在传统概念中,曲线的数维是1维,正方形是2维的。详细介绍见:维基百科:皮亚诺曲线
1. 问题描述
皮亚诺曲线是一条平面内的曲线,下图给出了皮亚诺曲线的 1 阶情形,它是从左下角出发,经过一个 3 × 3 的方格中的每一个格子,最终到达右上角的一条曲线。
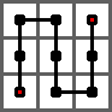
下图给出了皮亚诺曲线的 2 阶情形,它是经过一个 32 × 32 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。
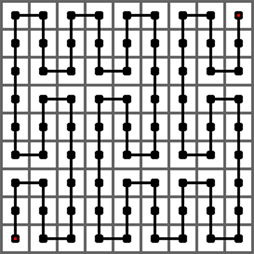
下图给出了皮亚诺曲线的 3 阶情形,它是经过一个 33 × 33 的方格中的每一个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发,最终到达右上角。
问题:求给定阶数的皮亚诺曲线中任意两个相邻点数值差之和。比如:
$1$ 阶皮亚诺曲线所有相邻点差值和为 $24$.
$2$ 阶皮亚诺曲线所有相邻点差值和为 $816$.
比赛中题目最后要求的是 $n = 14$ ,即求 $14$ 阶皮亚诺曲线中任意两个相邻点数值差的和。
2. 问题分析
首先,如果通过暴力打表,然后将所有相邻点差值的和累加起来,当然是不现实的。想想空间复杂度和时间复杂度就明白了。这里我们能够很容易得到空间复杂度是 $O((3^n)^2)$,估算一下当 $n = 14$ 时,内存至少需要 $170445$ GB.
>>> (3 ** 14) ** 2 * 8.0 / 1024.0 / 1024.0 / 1024.0
170445.38598478585
别做梦了,暴力杯并不是所有题都是可以暴力的。
那这样的题目应该怎么做呢?虽然 $n = 14$ 我们做不到,但是 $n$ 比较小的时候还是能够处理的嘛。比如:$n = 1$, $n = 2$ 这样的。先写一个模拟出来,再找找规律看看。(其实这样的一个解题思路基本上是么得问题的。)
对于这个东西该怎么模拟呢,请先看下面两张图,分别为 $1$ 阶皮亚诺曲线和 $2$ 阶皮亚诺曲线大致走向示意图。
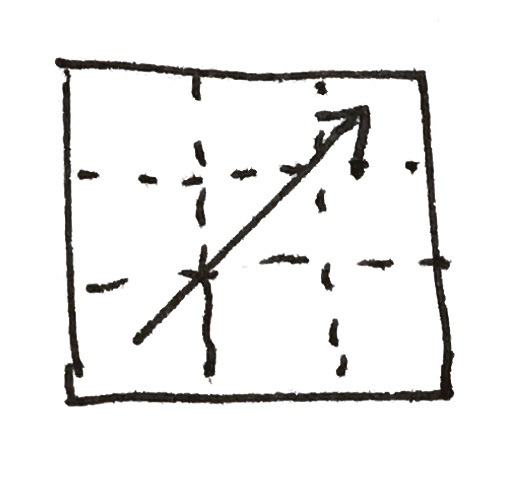
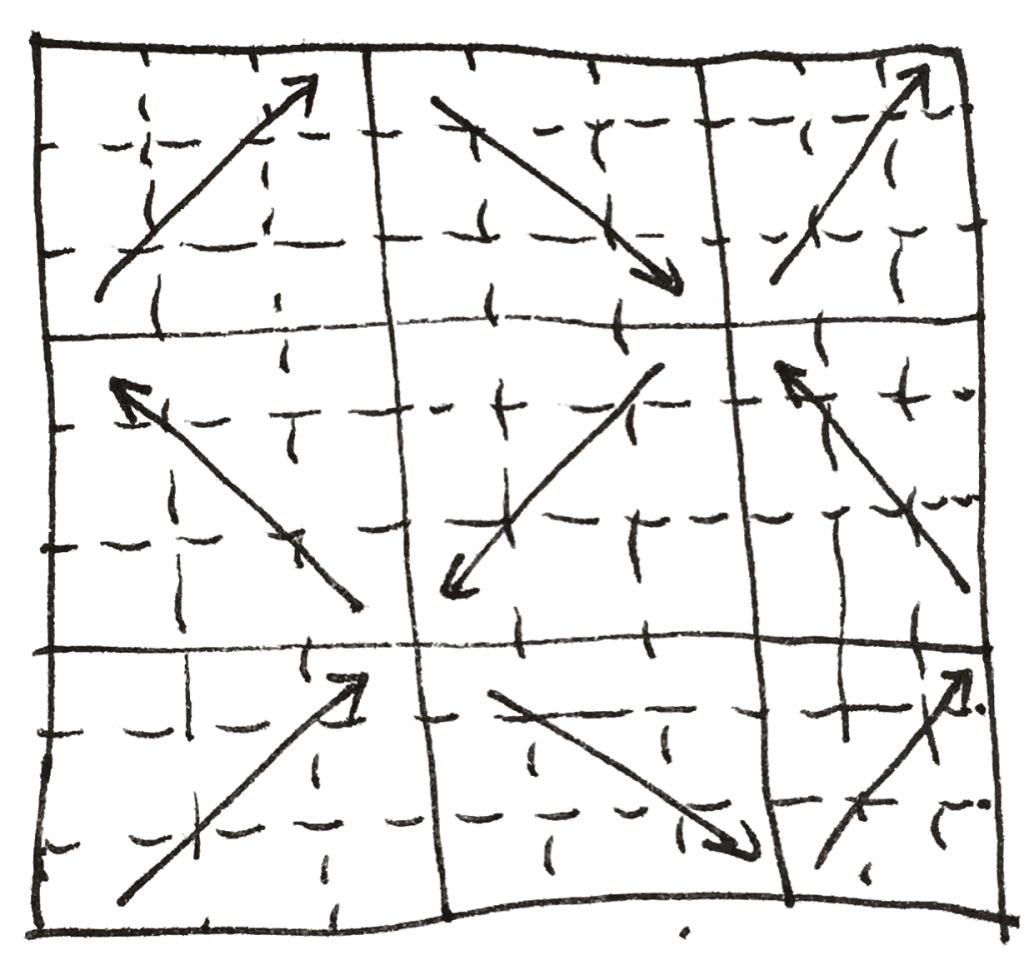
我们发现在所有的皮亚诺曲线中,大致走向只有四个方向:↗️、↖️、↘️、↙️,依次编号为1,2,3,4.
- ↗️
- ↖️
- ↘️
- ↙️
而皮亚诺曲线升阶(比如1阶变到2阶)过程,就是对基阶皮亚诺曲线进行扩展操作。比如我们看 $1$ 阶升阶为 $2$ 阶就是对↗️走向扩展为 9 个走向↗️↖️↗️ ↘️↙️↘️ ↗️↖️↗️. 到这里如果都能看明白,其他对这个题目解题就很有帮助了。我们接下来要做的就是将四个方向扩展出来的方向列表搞出来,这个可以从二阶扩展到三阶的皮亚诺曲线中得到。
- ↗️ 扩展为 ↗️↖️↗️ ↘️↙️↘️ ↗️↖️↗️ 对应编号为
121 343 121 - ↖️ 扩展为 ↖️↗️↖️ ↙️↘️↙️ ↖️↗️↖️ 对应编号为
212 434 212 - ↘️ 扩展为 ↘️↙️↘️ ↗️↖️↗️ ↘️↙️↘️ 对应编号为
343 121 343 - ↙️ 扩展为 ↙️↘️↙️ ↖️↗️↖️ ↙️↘️↙️ 对应编号为
434 212 434
到这里接下来就变得简单了,当然还有一点需要处理,那就是各个大致行走方向怎么接上的问题,比如:先↗️走,接下来需要↖️走,但是我应该怎样让↗️结束后的那个位置接上↖️开始的位置呢?
那么我们对于所有可能的组合进行的表示(当然并不是所有的方向组合都在这个方向中的,比如↗️接下来就不可能是↙️):
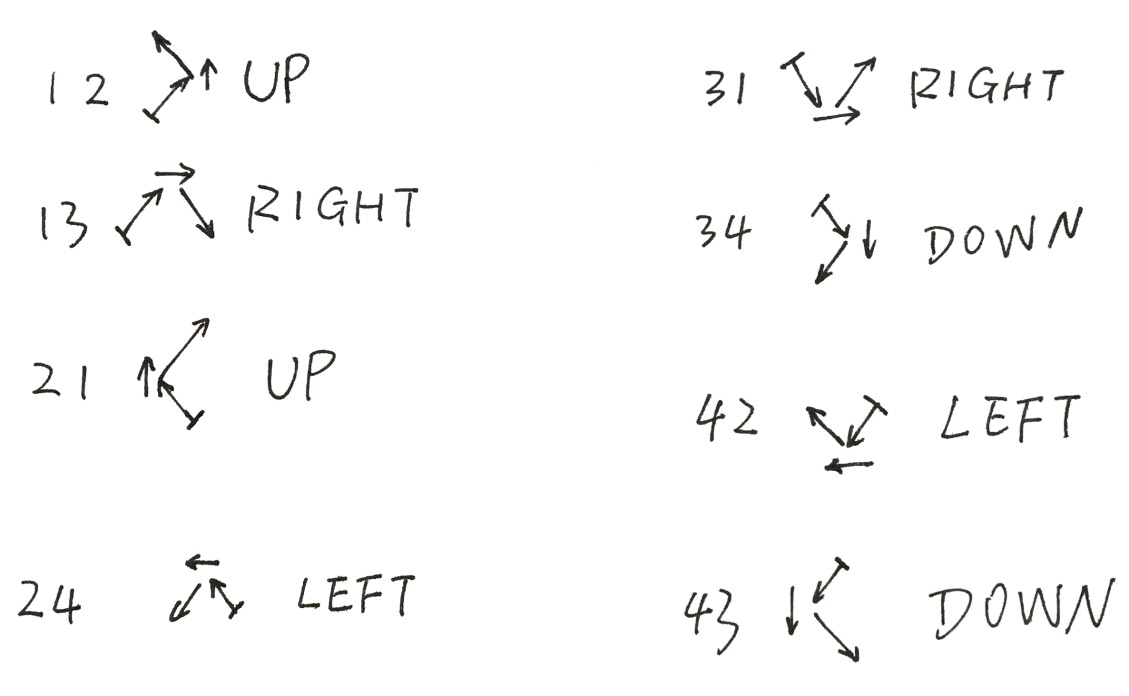
那对于大致方向与大致方向之间的连接关系我们也得到了。
下来就是把大致方向(↗️、↖️、↘️、↙️)表示成详细的行走方向(⬆️、⬇️、⬅️、➡️)即可。
3. 皮亚诺曲线实现
Dir.java 详细行走方向类,后面需要用到。
public class Dir {
public int ic;
public int jc;
public Dir(int _ic_, int _jc_) {
this.ic = _ic_;
this.jc = _jc_;
}
}
DirUtil.java 方向处理工具类,核心部分,用于升阶扩展操作,以及将大致行走方向表示成详细的行走方向。
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class DirUtil {
private static final Dir UP = new Dir(1, 0);
private static final Dir DOWN = new Dir(-1, 0);
private static final Dir RIGHT = new Dir(0, 1);
private static final Dir LEFT = new Dir(0, -1);
public static Dir[] dir1 = new Dir[]{
UP, UP, RIGHT, DOWN, DOWN, RIGHT, UP, UP
};
public static Dir[] dir2 = new Dir[]{
UP, UP, LEFT, DOWN, DOWN, LEFT, UP, UP
};
public static Dir[] dir3 = new Dir[]{
DOWN, DOWN, RIGHT, UP, UP, RIGHT, DOWN, DOWN
};
public static Dir[] dir4 = new Dir[]{
DOWN, DOWN, LEFT, UP, UP, LEFT, DOWN, DOWN
};
public static Dir[] getDir(DirTester.Point s, DirTester.Point t) {
if (s.x < t.x && s.y < t.y) return dir1;
if (s.x < t.x && s.y > t.y) return dir2;
if (s.x > t.x && s.y < t.y) return dir3;
return dir4;
}
public static Dir[] getDirById(int __id__) {
switch (__id__) {
case 1:
return dir1;
case 2:
return dir2;
case 3:
return dir3;
case 4:
return dir4;
}
return null;
}
// 升阶扩展操作
public static List<Integer> expandDirGroup(List<Integer> list) {
List<Integer> expandedList = new ArrayList<>();
for (int item : list) {
switch (item) {
case 1:
expandedList.addAll(Arrays.asList(1, 2, 1, 3, 4, 3, 1, 2, 1));
break;
case 2:
expandedList.addAll(Arrays.asList(2, 1, 2, 4, 3, 4, 2, 1, 2));
break;
case 3:
expandedList.addAll(Arrays.asList(3, 4, 3, 1, 2, 1, 3, 4, 3));
break;
case 4:
expandedList.addAll(Arrays.asList(4, 3, 4, 2, 1, 2, 4, 3, 4));
break;
}
}
return expandedList;
}
// 将大致行走方向展开为完整的行走方向
public static List<Dir> expandAsStepList(List<Integer> dirGroupList) {
List<Dir> dirs = new ArrayList<>();
int prevDirId = 0;
for (int dirGroupId : dirGroupList) {
Dir[] dirsTmp = getDirById(dirGroupId);
switch (prevDirId * 10 + dirGroupId) {
case 12:
case 21:
dirs.add(UP);
break;
case 13:
case 31:
dirs.add(RIGHT);
break;
case 24:
case 42:
dirs.add(LEFT);
break;
case 34:
case 43:
dirs.add(DOWN);
break;
}
assert dirsTmp != null;
dirs.addAll(Arrays.asList(dirsTmp));
prevDirId = dirGroupId;
}
return dirs;
}
}
HilbertCurveTester.java 则是对曲线结果进行测试了。
import java.util.*;
public class HilbertCurveTester {
static class Point {
public int x, y;
public Point() {
}
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
public static int[][] genMap(int level) {
if (level < 1) {
return null;
}
int mapSize = pow(3, level);
int[][] a = new int[mapSize][mapSize];
List<Integer> dirGroupList = new ArrayList<>();
dirGroupList.add(1);
for (int i = 2; i <= level; i++) {
dirGroupList = DirUtil.expandDirGroup(dirGroupList);
}
List<Dir> dirList = DirUtil.expandAsStepList(dirGroupList);
int x = 0;
int y = 0;
int val = 1;
a[x][y] = val++;
for (Dir dir : dirList) {
x += dir.ic;
y += dir.jc;
a[x][y] = val++;
}
return a;
}
public static int pow(int a, int n) {
int ans = 1;
for (int i = 0; i < n; i++) {
ans *= a;
}
return ans;
}
public static void display(int[][] a) {
for (int i = a.length - 1; i >= 0; i--) {
for (int j = 0; j < a[i].length; j++) {
System.out.printf("%2d ", a[i][j]);
}
System.out.println();
}
}
public static void main(String[] args) {
System.out.print("[n] > ");
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[][] a = genMap(n);
int sum = 0;
assert a != null;
display(a);
}
}
[n] > 1
3 4 9
2 5 8
1 6 7
[n] > 2
21 22 27 28 33 34 75 76 81
20 23 26 29 32 35 74 77 80
19 24 25 30 31 36 73 78 79
18 13 12 43 42 37 72 67 66
17 14 11 44 41 38 71 68 65
16 15 10 45 40 39 70 69 64
3 4 9 46 51 52 57 58 63
2 5 8 47 50 53 56 59 62
1 6 7 48 49 54 55 60 61
4. 问题求解过程
接下来我们就可以对生成的皮亚诺曲线进行找规律了,我们可以将所有距离都打了出来,形成一个 $(距离,个数)$ 表示形式。比如:
[n] > 1
(1, 8)
(5, 2)
(3, 2)
与给的样例是一样的 $1 \times 8 + 5 \times 2 + 3 \times 2 = 24$
[n] > 2
(1, 80)
(3, 20)
(5, 20)
(11, 6)
(13, 6)
(31, 2)
(33, 2)
(35, 2)
(37, 2)
(39, 2)
(41, 2)
这里与给的样例计算结果也是一样的。
我发现接下去打表就更长了,规律不好找了。于是我突发奇想,我想着直接把同样个数的数值都给加起来看看。
于是就有了以下关于不同 $n$ 的计算式子:
1 (24) => 1*8 + 8*2
2 (816) => 1*80 + 8*20 + 24*6 + 216*2
3 (23496) => 1*728 + 8*182 + 24*60 + 216*20 + 648*6 + 5832*2
4 (647520) => 1*6560 + 8*1640 + 24*546 + 216*182 + 648*60 + 5832*20 + 17496*6 + 157464*2
5 (17601144) => 1*59048 + 8*14762 + 24*4920 + 216*1640 + 648*546 + 5832*182 + 17496*60 + 157464*20 + 472392*6 + 4251528*2
6 (476293776) => 1*531440 + 8*132860 + 24*44286 + 216*14762 + 648*4920 + 5832*1640 + 17496*546 + 157464*182 + 472392*60 + 4251528*20 + 12754584*6 + 114791256*2
接下来就是快乐的找规律时间了。
我们将乘法左右给拆分出来,分成两个列表 list1 和 list2
list1
1 (24) => 1 8
2 (816) => 1 8 24 216
3 (23496) => 1 8 24 216 648 5832
4 (647520) => 1 8 24 216 648 5832 17496 157464
5 (17601144) => 1 8 24 216 648 5832 17496 157464 472392 4251528
6 (476293776) => 1 8 24 216 648 5832 17496 157464 472392 4251528 12754584 114791256
list2
1 (24) => 8 2
2 (816) => 80 20 6 2
3 (23496) => 728 182 60 20 6 2
4 (647520) => 6560 1640 546 182 60 20 6 2
5 (17601144) => 59048 14762 4920 1640 546 182 60 20 6 2
6 (476293776) => 531440 132860 44286 14762 4920 1640 546 182 60 20 6 2
至此,规律就变得很容易找了。
这里就不去过多赘述了。见下面的代码吧。
5. 解题代码
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static long pow(long a, int n) {
long ans = 1;
for (int i = 0; i < n; i++) {
ans *= a;
}
return ans;
}
public static List<Long> genList1(int n) {
if (n < 1) {
return new ArrayList<>();
}
if (n == 1) {
List<Long> result = new ArrayList<>();
result.add(1L);
result.add(8L);
return result;
}
List<Long> prev = genList1(n - 1);
List<Long> result = new ArrayList<>(prev);
result.add(result.get(result.size() - 1) * 3);
result.add(result.get(result.size() - 1) * 9);
return result;
}
public static List<Long> genList2(int n) {
if (n < 1) {
return new ArrayList<>();
}
if (n == 1) {
List<Long> result = new ArrayList<>();
result.add(8L);
result.add(2L);
return result;
}
List<Long> prev = genList2(n - 1);
List<Long> result = new ArrayList<>();
result.add(pow(9, n) - 1);
result.add(result.get(result.size()- 1) / 4L);
result.add(prev.get(1) * 3);
for (int i = 1; i < prev.size(); i++) {
result.add(prev.get(i));
}
return result;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
List<Long> list1 = genList1(n);
List<Long> list2 = genList2(n);
long ans = 0;
for (int i = 0; i < n * 2; i++) {
ans += list1.get(i) * list2.get(i);
}
System.out.println(ans);
}
}